Algebra involves the study of numbers in terms of their functions and relations.  In mathematics, a formal language, we use numerals to represent known or specified numbers, and letters to represent unknown or unspecified numbers.

In English, a natural language, we use names or proper nouns to represent known or specific individuals, and pronouns to represent unknown or unspecified individuals.  The Montessori student learns proper use of the English language while interacting with physical objects represented by the proper nouns and pronouns of English, not by employing some other natural language as a metalanguage in which to discuss the English language.  (It is generally poor practice to use a natural language, which the student has substantially mastered, as a metalanguage in which to study a second natural language. Such practice usually results in the student translating expressions from the second language into the first language for processing, rather than learning to think and speak fluently in the second language.  A similar practice, using English as a metalanguage in which to study the language of mathematics, is even more costly to the student.)

The following is an explanation of how the student learns algebra while interacting with manipulatives, physical objects, represented by the numerals and variables of mathematics.  For simplicity here, the explanation is given in two dimensions.  Of course, the youngest students interact with perceptual three-dimensional objects, concrete rectangular prisims, rather than with imaginary two-dimensional objects, abstract rectangles.  

1.    The proper interpretation of a numeral by answering three questions:

• How many objects?
• What base?
• In how many dimensions?

Here we have a unit square, it is one unit in two dimensions, in width and in length.  We use numerals to name specific numbers in mathematics (just as we use proper names to name specific objects in English). *^{1 N.B.}   We can name this object “one unit-square”, “(1 × 1²)”, “one unit”, or simply “1”.
 
 
 
How many? ... 1.     What base? ... 1.     In how many dimensions? ... 2.          (1 × 1²) = 1
 
 
Here we have five unit-squares.  We can name these objects “five unit-squares”, “(5 × 1²)”, “five units”, or simply “5”.  Alternatively, we have one bar consisting of five unit-squares, i.e., a bar five units in width and one unit in length.  Thus, we can name this object “one five-one-way”, “(1 × 5¹)”, “one five-bar”, or simply “5”.
 
 
 
How many? ... 5.     What base? ... 1.     In how many dimensions? ... 2.          (5 × 1²) = 5
How many? ... 1.     What base?     5.     In how many dimensions? ... 1.          (1 × 5¹) = 5
 
 
Here we have another bar.  It is one unit in length, but its width is not divided into units, so it doesn't have a specified width.  Since the name of the width does not represent a specified number, the interpretation or value given to that name may change or vary; so that name is a variable.  We use variables to name unspecified numbers in mathematics (just as we use pronouns to name unspecified objects in English).  We use letters as variables in mathematics.  We name the width of this object “x” because we can't count it as any specific number of units.  Thus, we have a bar x units in width and one unit in length.  We name this object “one x-one-way”, “(1 × x¹)”, “one x-bar”, or simply “x”.
 
 
 
How many? ... 1.     What base? ... x.     In how many dimensions? ... 1.        (1 × x¹) = x
 
 
We can now regard our unit square as a bar, in base x, that measures x in no (zero) dimensions.  We can now name this object “one x-no-way”, “(1 × x⁰)”, “one unit”, or simply “1”.
 
 
 
How many? ... 1.     What base? ... x.     In how many dimensions? ... 0.        (1 × x⁰) = 1
 
 
Likewise, we can rename this object, in base x, as “five x-no-way”, “(5 × x⁰)”, “five units”, or simply “5”.
 
 
 
How many? ... 5.     What base? ... x.     In how many dimensions? ... 0.        (5 × x⁰) = 5
 
 
Here we have three bars in base x.  We name this object  “three x-one-way”, “(3 × x¹)”, “three x-bars”, or simply “3x”.
 
 
 
How many? ... 3.     What base? ... x.     In how many dimensions? ... 1.        (3 × x¹) = 3x
 
 
We can arrange nine units in two dimensions so that we have a rectangle that is three wide and three long, or a square.  We name this object “three-units squared”, “(3 × 3)”, “one three-two-ways”, “(1 × 3²)”, “one three-square”, or simply “3²”.
 
 
 
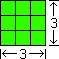
How many? ... 1.     What base? ... 3.     In how many dimensions? ... 2.        (1 × 3²) = 3²
 
 
Here we have a rectangle that is x wide and x long.  It is x in two dimensions, and we name it “x-squared”, “(x × x)”, “one x-two-ways”, “(1 × x²)”, “one x-square”, or simply “x²”.
 
 
 
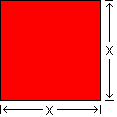
How many? ... 1.     What base? ... x.     In how many dimensions? ... 2.        (1 × x²) = x²
 
 
 
2.    The construction of compound (polynomial) numbers, and the composition of compound numerals (polynomials):
 
 
 Here is two x-bars plus four units, named “(2x + 4)”:
 
 
 
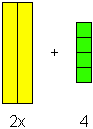
 How many? ... (2, 4).     What base? ... x.     In how many dimensions? ... (1, 0).
 
(2x¹ + 4x⁰) = (2x + 4)
 
 
Here is one x-square plus three x-bars plus two units,  written “(x² + 3x + 2)”:
 
 
 
How many? ... (1, 3, 2).     What base? ... x.     In how many dimensions? ... (2, 1, 0).
 
(1x² + 3x¹ + 2x⁰ ) = (x² + 3x + 2)
 
 
Here is two x-squares plus five x-bars plus four units, which we name “(2x² + 5x + 4)”:
 
 
 
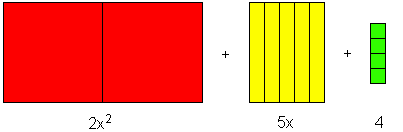
How many? ... (2, 5, 4).     What base? ... x.     In how many dimensions? ... (2, 1, 0).
 
(2x² + 5x¹ + 4x⁰) = (2x² + 5x + 4)
 
 
 
3.    The factoring of polynomial numbers:
 
 
In arithmetic and algebra we often need to find the factors of a number to solve a problem.  The factors of a number are two or more numbers which, multiplied together, are that number.  For example, 3 and 2 are factors of 6, because 3 times 2 is 6.  *^{2 N.B.}
 
Using manipulatives we can find the factors of a number by reconstructing a bar of unit squares into a rectangle of unit squares.  Here are the factors of 6:
 
 
 
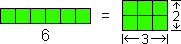
We can represent this fact with the expression, “6 = (3 × 2)”.
 
 
Since the trinomial “(x² + 3x + 2)” names a compound number constructed of three groups of rectangular parts, we can find the factors of this number by reconstructing the rectangular parts into a single rectangle.  The factors are the resulting rectangle's width and length, (x + 2) and (x + 1).
 
 
 
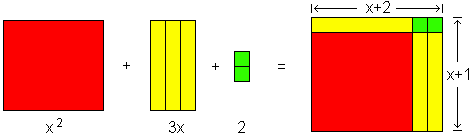
To represent this fact we write “(x² + 3x + 2) = (x + 2) (x + 1)”.
 
 
Let's factor the number, (x² + 5x + 6).  First we group the blocks so that each group is represented by a part of the trinomial.  Then we reconstruct this row of grouped blocks into a single rectangle, and find the width and length of the rectangle, which are the factors of the number.
 
 
 
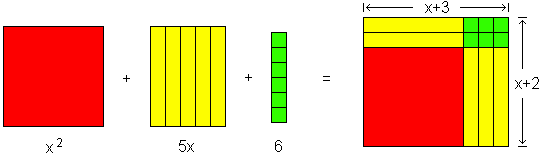
The sentence that represents this fact is “(x² + 5x + 6) = (x + 3) (x + 2)”.
 
 
 
4.    Higher dimensions and definite bases:
 
 
After the Montessori student learns to factor polynomial numbers and perform basic operations in two dimensions, such as addition, subtraction, multiplication, division, and square roots, using manipulatives, he may then use three-dimensional blocks, in base x, to perform basic operations, such as addition, subtraction, multiplication, division, and cube roots.
 
Having mastered these algebraic manipulations and notations, the student may substitute a definite base (such as base ten) for base x.  He then discovers how to perform these same operations using multidigit, composed numerals, in a number system incorporating place value to facilitate working with large numbers.  Such a student does not require “lessons” or “demonstrations” of traditional Montessori math equipment.  He discovers for himself how to do long division or how to calculate a square root.
 
The joys of such discoveries are even available to primary-level students who have not yet acquired the perceptual ability to distinguish a numeral “2” from a numeral “5”, or a numeral “6” from a numeral “9”.  Such students can master basic operations, such as long division and square roots, using only the digits (“0” “1” “2” “3”) of the base-quad number system, before they can reliably decode the ten digits (“0” “1” “2” “3” “4” “5” “6” “7” “8” “9”) required to operate in the base-ten number system.  By having their learning environments enriched with base-quad Montessori math materials, students will not be prevented by limitations of traditional, base-ten materials from developing mathematical aptitudes during earlier and more fruitful “sensitive periods” for the acquisition of those aptitudes.
 
 
 
5.    Multiple bases –  working with more than one variable:
 
 
As the student employs this knowledge of algebraic operations using expressions with a single variable to the task of mastering arithmetic, he also extends his study of algebra to numbers incorporating several variables.  To build these numbers he requires additional blocks with distinct lengths and widths representing additional unspecified numbers (y, z, etc.) which may vary in value from both x and 1.
 
 
Now let's factor the number (x² + 2x + 2xy + y² + 2y + 1).  First construct the blocks into groups, each of which is represented by a part of the polynomial.  Then we reconstruct the row of grouped blocks into a rectangle, and find the width and length of the rectangle, which are the factors of the number.  In this case we get a square, bearing an unmistakable similarity to the face of the trinomial cube found in many Montessori classrooms.
 
 
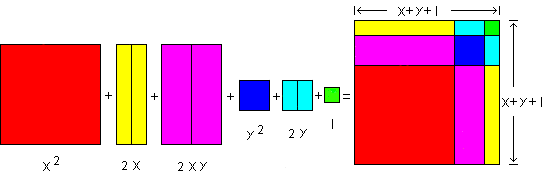
The sentence that specifies this fact is “(x² + 2x + 2xy + y² + 2y + 1) = (x + y + 1)²”.
 
  *¹  N.B.:
 
In order to derive the maximum benefit from interaction with a specially prepared Montessori environment,  it is crucial that the student not confuse the concept of a numeral – ‘a name of a number’ (which is a word from the language of mathematical discourse), with the concept of a number – ‘a quantity or measure’ (which is an object from the universe of mathematical discourse).

Confusion of word with object is a more serious problem for the young student of mathematics than for the young student of English.  Despite our imprecise usage of English, the student is not very apt to confuse a tree, which he can learn to climb, with “tree”, which he can learn to pronounce, spell, write, and read.  If we mistakenly ask him to put mom on the blackboard, he will probably reach for the chalk rather than reach for his mother, but we had better not ask him to put paint on the blackboard unless we are prepared to learn an expensive, albeit valuable and well deserved, lesson!  However, he is more apt to confuse 1 and 2, from which he can construct 3, with “1” and “2”, from which he can compose “21” or “12”.  (He may learn to avoid this latter confusion by unconscious attention to context, but even world-renowned mathematicians have been known to confuse a material conditional with an implication.)

When working with a very young mathematician, who has not yet developed the level of auditory discrimination necessary to reliably distinguish between the sounds of  the spoken words “number” and “numeral”, it is preferable to use language which will not contribute to the student's confusion:
 
        Vocalize the expression “construct (x + 2)” as “construct the number, x plus two”.
 
        Vocalize the expression “compose “(x + 2)” ” as “compose the name of  x plus two”.
 
        Do not vocalize “compose “(x + 2)” ” as “compose the numeral for  x plus two”.
 

[Back to *1 in main text above]

*²  N.B.:
 
In order to derive the maximum benefit from interaction with a specially prepared Montessori environment,  it is crucial that the student not confuse the concept of similarity or equivalence – ‘the same in some respect(s)’ (which constitutes joint membership in a set or class) – with the concept of identity – ‘the same in all respects’ (which constitutes being one and the same object).
 
“(3 × 2)” and “6” are two different names (numerals) for the same object (the number 6).  These two names are similar names, in that they each name the same object; they are equivalent names, in that they each take the same object as their semantic value.  However, they are not identical names.
 
We can represent such facts with metamathematical equivalency statements about the numerals (the names) that we use to refer to numbers:
 
        “ “(3 × 2)” names the same number that “6” names ”,
 
        “ “(3 × 2)” is equivalent to “6” ”,
 
        “ “(3 × 2)” ≡ “6” ”,  or
 
        “ “(3 × 2)” equals “6” ”.
 
Usually, however, we simply represent such facts with mathematical identity statements about the actual numbers (the objects) themselves:
 
        “ (3 × 2) is the same number as 6 ”,
 
        “ (3 × 2) is identical to 6 ”,
 
        “ (3 × 2) = 6 ”,  or
 
        “ (3 × 2) is 6 ”.
 
Therefore, whenever vocalizing  mathematical expressions (identity statements or equations), it is preferable to use language which will not contribute to the student's confusion:
 
        Vocalize the expression “1 + 1 = 2” as “one plus one  is  two”.
 
        Do not vocalize “1 + 1 = 2” as “one plus one  equals  two”.
 

 [Back to *2 in main text above]

[BACK] Copyright © 1978 by College of Early Learning.